Представим себе, что в космосе в гиперпространстве требуется отремонтировать антенну в виде гиперкуба, с ребром a, состоящую элементарных кубов 1ⁿ в общем количестве aⁿ. Благодаря своей уникальной геометрии эта антенна, простирающаяся на несколько километров, может передавать принимать сигналы в гиперполе.  Командир корабля подозревает неполадки в вершине гиперкуба, как раз по направлению к  Альфа Центавра, и даёт нам задание исследовать ситуацию детальнее на месте.

Попробуем вместе предпринять путешествие к вершине гиперкуба в n-мерном пространстве на реактивном ранце. Движение начинается из  центра гиперкуба, где расположен корабль. Из-за технических ограничений двигаться можно только под прямыми углами. Цель состоит а ремонте поломанной вершины гиперкуба. Как скоро мы достигнем вершины гиперкуба?

Стартуя из центра гиперкуба, находящемся как раз в начале координат, мы сначала достигнем любой  грани, на которой расположена поломанная вершина. При этом первый «прыжок» нашего маршрута приведёт нас прямо в центр грани. Здесь мы обнаружим, что оказались в центре гиперкуба размерности n — 1. Далее мы выберем направление для следующего пряжка к желаемой грани этого гиперкуба и  будем продолжать свой затяжной прыжок до тех пор, пока не достигнем одномерного ребра, и наконец, самой дефектной вершины. Всего таких прыжков будет n.

 

С позиции командира корабля, наблюдающего за нашими перемещениями из из центра антенны в виде гиперкуба, каждый следующий наш прыжок, кроме первого, совершается в гиперплоскости, и каждый раз в направлении ортогональном всем предыдущим прыжкам. Такое положение дел совершенно естественно для n-мерного наблюдателя.

Предположим для наглядности, что исходная размерность пространства была равна 4. Гиперкуб размерности 4 — это тессера́кт. Гипотетическое многомерное существо на первом своем прыжке достигнет центра трёхмерной грани или куба, далее — совершит прыжок на центр двумерной грани или квадрата, далее — на одномерное ребро и наконец — к вершине. Всего n прыжков для общего n- мерного случая. 

 Интернет изобилует рисунками и видео клипами с изображением многомерных гиперкубов, их проекциями на двумерную плоскость, расположенную перед глазами обычного человека — существа  трехмерного пространства. Благодаря эффекту параллакса можно увидеть достаточно любопытные структуры. Но одного любопытства недостаточно - требуется аналитическое мышление, которое поможет ощутить красоту гиперкуба, и как косвенный результат - «увидеть» наглядное решение Великой Теоремы Ферма. - Попробуем? 

Вот небольшой тест для сампроверки: каковая общая длина пути нашего путешествия из начала координат к вершине? Ребро гиперкуба равно а киломотров. Для поиска ответа на вопрос, вспомним, что каждый шаг перпендукулярен другим, всего шагов n и примирим Теорему Пифагара. И мы получим . . . .    ½ a√n

К доказательству Великой Теоремы Ферма через гиперкубы

Гиперкуб обладает свойством симметрии. Если расположить начало координат в центре  гиперкуба, то каждая его вершина будет находится на расстоянии ½ a√n, что легко вычисляется по теореме Пифагора. Перпендикуляр, опущенный из центра гиперкуба на любую его грань, проходит через её центр и длина образуемого отрезка (высоты любой из совершенно одинаковых из 2n гиперпирамид, на которые рассекается гиперкуб) составляет  ½а. Легко убедиться, что грань гиперкуба – это гиперкуб размерности на единицу меньше, также имеющий грани-ребра размерности n-2, n-3 …вплоть до одномерных ребер и нольмерных вершин (для случая пространства целых чисел роль вершин принимают на себя единичные  кубы или гиперкубики 1ⁿ ). Грань гиперкуба располагается в гиперплоскости, перпендикулярной только что построенной высоте и проходящей через основание этой  высоты – точку пересечения прямой, исходящей из начала координат ортогонально  грани гиперкуба с этой гранью. Образно говоря, с позиции гипотетического  n- мерного существа, все грани гиперкуба воспринимаются  не как объемные, а как плоские фигуры.

  

Почти четыре столетия мир бился над решением Теоремы Ферма. Есть доказательство в 140 страниц Эндрю Уайлса  для специалистов в теории чисел, но его невозможно пересказать. Попробуем рассмотреть теорему Ферма с позиции физики и геометрии. Именно с этих позиций позиций Пьер де Ферма смог найти решение, основные идеи которого схематично уместились бы на достаточно широких полях книги, в нескольких рисунках.  Скептики продолжают считать, что Пьер де Ферма, вероятнее всего, заблуждался. Между тем, последовательное применение основных принципов физики, геометрии, мысленного эксперимента заставляют думать иначе.  История открытия  теоремы Ферма должна стать частью школьной / вузовской подготовки. В  самом деле, суть доказательства укладывается в одной формуле и одном рисунке.

 

 

 

Главная идея найденного Маратом Авдыевым доказательства (всего найдено автором три способа доказательства) состоит в том, что условия равенства объёмов множества слоёв гиперкубов вписанных друг в друга в уравнении Ферма: aⁿ = cⁿ - bⁿ  и свойство симметрии фигуры в пространстве целых чисел взаимно исключают друг друга. Для доказательства, помимо свойства симметричности фигуры в виде вложенных гиперкубов a, b и c использовался принцип однородности пространства, постулируемый Евклидовой геометрией.

 

 

 

 Файл можно получить по ссылке: Монография 1.pdf https://yadi.sk/i/CK9zAAyQsd-15A Зебра, доклад на VII МЕЖДУНАРОДНЫЙ КОНГРЕСС СОЦИОЛОГОВ ТЮРКСКОГО МИРА

 «ЕВРАЗИЯ И ГЛОБАЛЬНЫЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЕ ИЗМЕНЕНИЯ» и др. В марте 2020 автор доказательства обратился в Роспатент с регистрацией Базы данных ЭВМ, кодирующей грани куба.

 

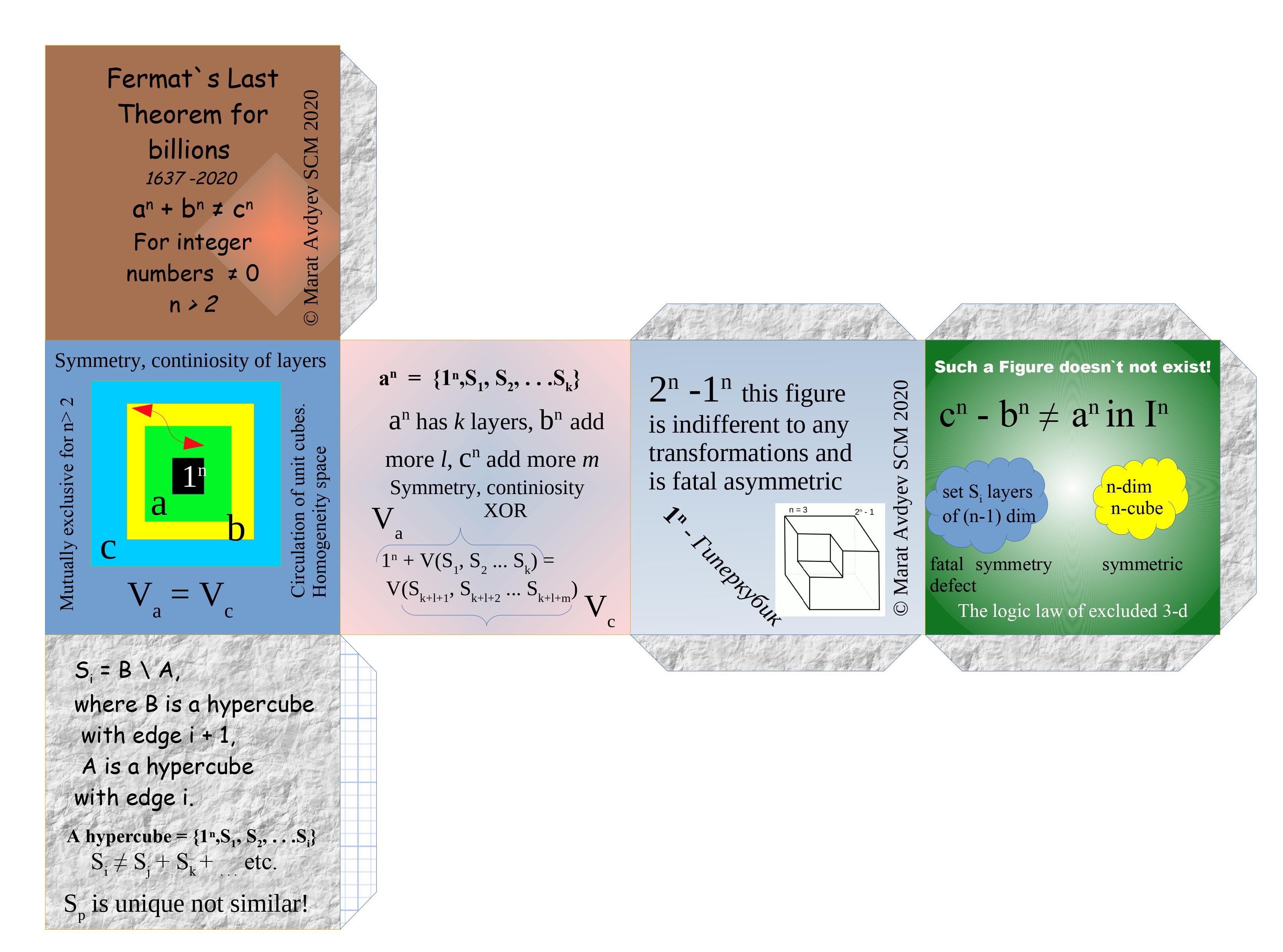
Однородность или неоднородность фигуры?

Несложные рассуждения приводят нас к мысли, что слои являются однородными для случая двумерного пространства — то есть квадратов и неоднородными для кубов и гиперкубов, при n ≥ 3. Этот вывод легко получить из свойства конгруэнтности:
=================================================
одна n- мерная фигура конкруэнтна другой тогда и только тогда, когда конгруэнтны все образующие фигуру элементы младших размерностей.
=================================================
Для гиперкуба это налагает требование конгруэнтности каждой (гипер)грани размерности k, где k – целое, пробегающее значение от 1 до n-1. Говоря проще, два куба (слоя) равны между собой, если и только если, равны все грани, рёбра младших размерностей.
Вспомним как во времена Фалеса сравнивались фигуры: совмещение, параллельный перенос, поэлементный обмен подобных частей, составляющих сравниваемые фигуры. Мы используем эти методы и спустя 2,5 тыс. лет, примеряя обувь либо одежду, прикладывая друг другу фотографии, совмещая 3D цифровые модели с целью поиска различий и т.д.
Внимательный взгляд на сечение вложенных друг в друга гиперкубов, образуемых на основе ряда натуральных чисел, показывает, что каждый слой является уникальным в том смысле, что Sj = Sk <=> j = k. Слои были бы подобны друг другу лишь в том случае, когда все их линейные размеры возрастали бы в равной пропорции по мере отдаления от начала координат и увеличения ребра i. Но толщины слоёв остаются постоянными из чего следует: слои изоморфны, но не подобны друг другу для случая n > 2:

А также готовится к печати Итерактивная наука с публикацией М.А. Авдыева.